Symétries Rotations Frises Pavages Coloriages

Les frises - Atelier - Exemples

Les frises sont des bandes décorées par la répétition régulière d'un motif selon une direction.
Prenons une frise et transformons la. Est-il encore possible de la superposer à la frise initiale?

Translation	Symétrie verticale	Symétrie horizontale	Rotation de 180°
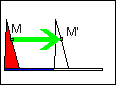
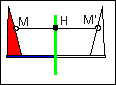
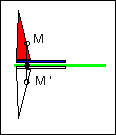
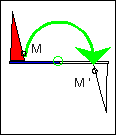
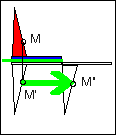
le motif est reporté à l'identique par glissement horizontal. Tout point M du motif est transformé en un point M' tel que MM'=constante.	Comme dans un miroir,tout point M du motif est transformé en un point M' tel que MH=HM', H étant un point de l'axe de symétrie ici vertical.	C'est la même transformation que précédemment, ici l'axe est horizontal .	Le centre O de rotation étant donné, tout point M du motif a une image M' telle que: OM=OM' et MOM'=180°.
La symétrie horizontale peut être une symétrie glissée:
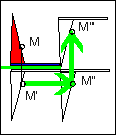
après avoir transformé le motif selon une symétrie par rapport à un axe horizontal, on obtient l'image finale en réalisant une translation horizontale et éventuellement verticale.

On peut trier les frises avec une notation utilisée en cristallographie. Cette notation utilise 4 caractères, chaque caractère indique la réponse à une question sur la frise.
caractère n°1: y a-t-il une translation qui laisse la frise inchangée?
oui=> le caractère n°1 est p; ce sera toujours p car les frises sont formées à partir d'une translation d'un motif.
caractère n°2: y a-t-il une symétrie par rapport à un axe vertical qui laisse la frise inchangée?
si oui=> le caractère n°2 est m; si non=>le caractère n°2 est 1.
caractère n°3: y a-t-il une symétrie par rapport à un axe horizontal qui laisse la frise inchangée?
si oui=> le caractère n°3 est m; si elle est glissée => le caractère n°3 est a; si non=>le caractère n°3 est 1.
caractère n°4: y a-t-il une rotation de 180° qui laisse la frise inchangée?
si oui=>le caractère n°4 est 2; si non=> le caractère n°4 est 1.

Voici une frise. Tentons de déterminer à quel type elle correspond.
Une marque jaune et une bleue ont été portées sur la frise comme repère. Lorsqu'on place le curseur sur la frise, on voit l'image après la transformation. Lorsque la frise reste inchangée après la transformation, cette transformtion est acceptée(oui).

Translation: oui=>p

Symetrie verticale: non=>1

Symetrie horizontale: non=>1

Rotation: oui=>2;

La frise peut-elle être inchangée après une :	Translation	Symétrie verticale	Symétrie horizontale	Rotation de 180°	type de frise
	oui=>p	non=>1	non=>1	non=>1	p111
	oui=>p	oui=>m	non=>1	non=>1	pm11
	oui=>p	non=>1	oui=>m	non=>1	p1m1
	oui=>p	non=>1	glissée=> a	non=>1	p1a1
	oui=>p	non=>1	non=>1	oui=>2	p112
	oui=>p	oui=>m	oui=>m	oui=>2	pmm2
	oui=>p	oui=>m	glissée=>a	oui=>2	pma2

Remarque: Toutes les combinaisons des 4 caractères ne sont pas représentées. Certaines ne peuvent exister. Par exemple, la sixième frise est de type pmm2. Il y a une translation(=>p), un axe de symétrie verticale(=>m), un axe de symétrie horizontale(=>m) qui laissent la frise inchangée.Ces conditions (pmm) entraînent qu'on pourra toujours trouver une rotation de 180°qui laisse la frise inchangée.Vous pouvez faire des dessins pour vous convaincre qu'il n'y a pas de pmm1. Il en est de même pour d'autres combinaisons( p1m2,pm12...n'existent pas).